Find the Ph of a Solution of 0.013 M Hno2
Attention:This post was written a few years ago and may not reflect the latest changes in the AP® program. We are gradually updating these posts and will remove this disclaimer when this post is updated. Thank you for your patience!
Abstract: pH is a unit of measurement often used in fundamental chemistry concepts. "How to Calculate pH" explains it's categories the scientific mathematics and role pH has in our lives.
Terms to Be Familiar With:
- pH
- pOH
- Hydrogen ion
- Hydroxide ion
- Acid
- Base
What is pH?
The term "pH" is an abbreviation for the "potential of hydrogen." pH is a unit of measurement which represents the concentration of hydrogen ions in a solution. This unit was introduced by biochemist Søren Peter Lauritz Sørensen in 1909. It was an easy way to represent the concentration of hydrogen ions in a solution during titrations. When an acid or base is added to water, that compound dissociates into ions. For acids one of those ions is a hydrogen ion (H+) and for bases one of the ions is a hydroxide ion (OH–). This description of acids and bases is known as the Arrhenius Theory. The concentration of hydrogen ions are often described by the pH scale as a numeric value.
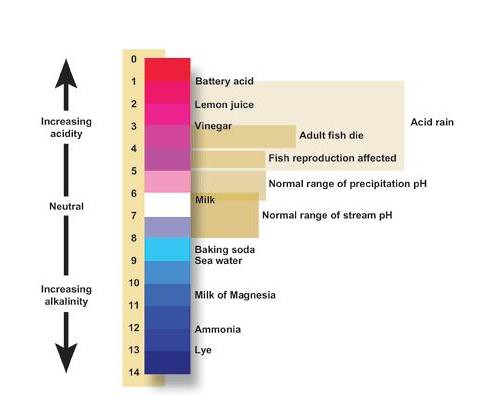
The pH Scale: Acidic, Neutral, and Basic
The pH scale describes the acidity of the solution: acidic, neutral, or basic A solution with a pH less than 7 is an acid, exactly 7 is a neutral solution, and above 7 is a base. Bases have less hydrogen ions but more hydroxide ions, represented by the pOH or "potential of hydroxide ions."
Table 1. The pH Scale
| Acidic | Neutral | Basic |
| Less than 7 | 7 | Greater than 7 |
Many other scientists studied the proprieties of acids and bases from the ideas of Sorensen and Arrhenius and came up with their own definitions. A notable theory is known as the Bronsted-Lowry Theory. The Bronsted-Lowry Theory is a concept involving acid and bases which suggest that acids act as proton donors. Since neutral hydrogen atoms are usually made of one proton and one electron, a positive hydrogen ion is often referred to as a proton. These protons carry a positive charge and are given away to the bases. Bases, with that logic, are proton acceptors. Bases, carrying lone pairs of electrons, attract positive hydrogen ions (protons).
In the lab, pH can be determined by a pH indicator such as pH paper. pH paper usually contains a weak acid or a weak base which will respond by changing color at a specific pH. This method is used frequently as a cheap, quick way to determine pH rather than using pH meters which need frequent calibration and maintenance. Keep in mind that very low or very high pH value solutions can be very caustic and should be handled with care.
Practice Problems
Determine if the following solution is acidic, neutral, or basic.
- pH = 1.00
- pH = 10.00
- pH = 6.99
- pH = 7.02
- pH = 8.00
- pH = 13.00
- pH = 2.00
Answers:
- Acidic
- Basic
- Neutral
- Neutral
- Basic
- Basic
- Acidic
Concentrations of H+ and OH–
Concentration is the amount of solute in respect to the amount of total solution. A high amount of solute equals a high concentration, where a lower amount of solute would equal a low overall concentration.
When an acid or a base is placed into a solvent, that compound will dissociate into ions. The concentration of H+ (hydrogen ions) in the solution will determine the acidity or basicity of the solution. A high concentration of H+ will signify an acidic solution and a low concentration of H+ will signify a basic solution.
In hydrochloric acid for example (a common acid that is an aqueous solution of HCl), HCl molecules have dissociated into two kinds of ions, H+ and Cl–. This dissociation produces a high H+ concentration, which is a property of an acidic solution.
The same can be seen in basic solutions where there is a low H+ concentration, due to the high
OH– (hydroxide ion). For example, when NaOH (sodium hydroxide, a common base), is placed in water, it dissociates into two kinds of ions, Na+ and OH–. The high OH– concentration, which corresponds to a low H+ concentration, is a property of basic solution.
Table 2. Relationship Between pH and pOH
| Concentration of H+ | Concentration of -OH | Example(s) | |
| Acid | High | Low | HCl, HCOOH, HNO3 |
| Base | Low | High | NaOH, MgO, CaCO3 |
| Neutral | Equal to OH– | Equal to H+ | Water |
The determination of pH and pOH will be calculated by using the concentration of hydrogen ions and hydroxide ions respectively. pH and pOH also have a relationship so that if you do not have enough information to determine one, you can use the concentration of the other. This will be done through Sorensen's equation for calculating pH.
How to Calculate pH
Note: Please use a scientific calculator.
pH is determined by the concentration of H+, which is frequently summarized as [H+]. This can be calculated by the following equation:
pH=-log { \left[ { H }^{ + } \right] } or pH=log { \left( \dfrac { 1 }{ \left[ { H }^{ + } \right] } \right) }
Conversely, the hydrogen concentration can be found by a given pH. The [H+] can be calculated by the following equation.
\left[ { H }^{ + } \right] ={ 10 }^{ -pH }
The determination of the concentration of hydrogen ions and pH will later be used to show the relationship between pH and pOH.
Key Equations:
pH=-log { \left[ { H }^{ + } \right] } or pH=log { \left( \dfrac { 1 }{ \left[ { H }^{ + } \right] } \right) }
\left[ { H }^{ + } \right] ={ 10 }^{ -pH }
Example 1: Calculate the pH of a 0.200 M HCl solution.
HCl solutions are strong acids, so we can already expect a pH less than 7. Using the 0.200 M HCl as the [H+] (concentration of hydrogen ions) the solution is as follows:
pH=-log { \left[ { H }^{ + } \right] } = log(0.200) =0.70
A 0.70 pH indicates a very acidic solution.
Example 2: Calculate the pH of a 0.100 M nitric acid solution.
Nitric acid has a chemical formula of HNO3. HNO3 is another strong acid, so the pH of this solution will also be less than 7. Using the 0.100 M nitric acid as the [H+] (concentration of hydrogen ions) the solution is as follows:
pH=-log { \left[ { H }^{ + } \right] } = log (0.100) = 1.00
A 1.00 pH indicates a very acidic solution.
In examples 1 and 2 we are able to use the concentration of the acid as the concentration of the H+ ion because every acid molecule dissociates, thereby releasing an H+ ion. These types of acids are referred to as "strong acids". For "weak acids", most of the acid molecules do not dissociate, so we would have to use more complex methods to calculate pH for solutions of weak acids. We'll stick to strong acids and bases in this article, and explore weak acids and base in another article.
Example 3. What is the hydrogen ion concentration of a solution that has a pH of 4.30?
This example provides the opposite information. Here, we are given the concentration of H+ in a solution and are asked to determine the pH.
4.30 = -log { \left[ { H }^{ + } \right] }
-4.30 = log { \left[ { H }^{ + } \right] }
\left[ { H }^{ + } \right] ={ 10 }^{ -4.30 }M=5.01x{ 10 }^{ -5 }M
How to Calculate pOH
pOH is determined by the concentration of OH–, [OH–]. This can be calculated by the following equation:
pOH=-log { \left[ { OH }^{ - } \right] } or pOH=log { \left( \dfrac { 1 }{ \left[ { OH }^{ - } \right] } \right) }
Conversely, the hydroxide concentration can be found by a given pOH. The [OH–] can be calculated by the following equation.
\left[ { OH }^{ - } \right] ={ 10 }^{ -pOH }
pOH is a different way of describing acidity and basicity, so be careful not to mix it up with pH. The descriptions for solutions based on the pOH scale are given in Table 2.
Table 3. The pOH Scale
| Basic | Neutral | Acidic |
| Less than 7 | 7 | Greater than 7 |
The determination of the concentration of hydroxide ions and pOH will be later used to show the relationship between pH and pOH.
Key Equations:
pOH=-log { \left[ { OH }^{ - } \right] } or pOH=log { \left( \dfrac { 1 }{ \left[ { OH }^{ - } \right] } \right) }
\left[ { OH }^{ - } \right] ={ 10 }^{ -pOH }
Example 1: Calculate the pOH of a 1.20 M NaOH solution.
This is calculated similarly to the determination of pH. Instead of determining the pH, we will be determining the pOH with use of -log[OH–]. NaOH will dissociate completely in solution, so we can use the concentration of NaOH as the concentration of OH–.
pOH=-log { \left[ { OH }^{ - } \right] } = log(1.20) = -0.08
A -0.08 pOH indicates a very basic solution.
Example 2: Calculate the pOH of a solution with a hydroxide concentration of 5.23 x 10-5 M.
pOH=-log { \left[ { OH }^{ - } \right] } = log(5.23 x 10^{-5}) = 4.20
Example 3. What is the hydroxide concentration of a solution that has a pOH of 11.30?
This example provides the opposite information. Here, we are given the concentration of OH– in a solution and are asked to determine the pOH. This is done similarly to the determination of hydrogen concentration from a pH.
11.30 = -log { \left[ { OH }^{ - } \right] }
– 11.30 = log { \left[ { OH }^{ - } \right] }
{ \left[ { OH }^{ - } \right] }={ 10 }^{ -11.30 }M=5.01x{ 10 }^{ -12 }
Calculate the Relationship Between pH and pOH
In the section "Concentrations of H+ and OH–" we discussed that the high concentration of hydroxide ions left little room for hydrogen ions and vice versa. The relationship of pH and pOH is that both values will equal 14.00. This can be represented in the following equation:
pH + pOH = 14.00
You can check your work by adding the pH and pOH to ensure that the total equals 14.00. This also is an excellent representation of the concept of pH neutrality, where equal concentrations of [H+] and [OH–] result in having both pH and pOH as 7.
pH+pOH=14.00
pH=14-pOH
pH=14-pH
Example 1: What is the pH of a solution that has a pOH of 12.40?
Keep in mind that the relationship of pH and pOH equals 14.
pH+pOH = 14.00
pOH = 12.40
pH= unknown
pH +12.40 = 14.00
pH =1.60
Check Your Work: 1.60 + 12.40 = 14.00
Example 2: What is the pOH of a solution that has a [H+] of 0.100 M HCl?
First, determine the pH and use that value with the relationship of pH and pOH.
pH+pOH = 14.00
pH = -log[0.1000] = 1.00
1.00 + pOH = 14.00
pOH = 13.00
Check Your Work: 1.00 + 13.00 = 14.00
Example 3: What is the pOH of a solution that has a pH of 3.40?
Keep in mind that the relationship of pH and pOH equals 14.00.
pH+pOH = 14.00
pH = 3.40
pOH = unknown
pOH+3.40 = 14.00
pOH=10.60 = pH 10.60
Check Your Work: 10.60 + 3.40 = 14.00
The Importance of pH
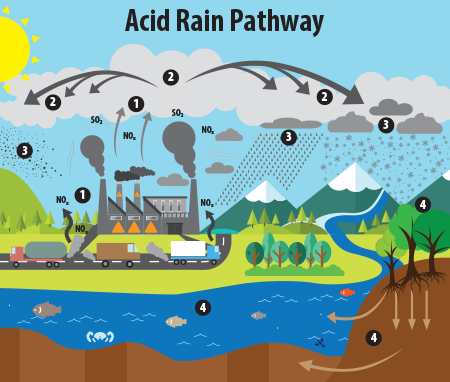
pH is all around us. It is important that vital solutions such as water, stomach acid, and blood maintain a consistent pH. Water, with a neutral pH of around 7, determines the solubility of many compounds. Without the appropriate pH of water, many chemical reactions would not occur. This can also be seen through naturally occurring phenomena such as acid rain. Highly acidic precipitation can cause erosion and other hazardous environmental outcomes.
pH plays an important role in the solutions in the human body. Specific pH values are vital to the roles of solutions such as saliva, stomach acid, and blood. The production of saliva in the mouth is known as the first step of digestion. Throughout the digestive tract, food must be broken down by acidic solutions. It is important that the pH of saliva should be between 6.5-7.5, slightly acidic, to begin this process. Later on, stomach acid functions in the digestive system as well. It is important that stomach acid has a very acidic pH, ranging from about 1.5 to 3.5, due to the secretion of HCl and the high concentration of hydrogen ions. This strongly acidic environment kicks digestion into high gear and begins to break down food particles in preparation for the excretion process.
Healthy blood has a pH of 7.4. Hundreds of reactions occur in the bloodstream, such as enzymes, which require a specific pH. Blood with a higher or lower pH can result in negative symptoms. Acidosis is a symptom of a condition in which the pH value of blood is too low and alkalosis indicates blood with a pH value which is too high.
Humans aren't the only organisms that rely on appropriate pH levels. Some species only thrive in alkaline (basic) environments and would not be able to survive in neutral or acidic environments. Entire ecosystems revolve around pH.
Questions for Discussion
- Why is it important that oceans keep a specific pH?
- Name some common household items with an basic pH.
- What is the pH of vinegar? Why?
- If a patient suffers from acidosis, what are they suffering from?
- How does pH play a role in the blood?
More with pH: Acid-Base Equilibrium, Titrations, Buffers, pKa, Equilibrium Constant, Neutralization, Conjugate Acids, Conjugate Base.
Looking for Chemistry practice?
Check out our other articles on Chemistry.
You can also find thousands of practice questions on Albert.io. Albert.io lets you customize your learning experience to target practice where you need the most help. We'll give you challenging practice questions to help you achieve mastery in Chemistry.
Start practicing here .
Are you a teacher or administrator interested in boosting Chemistry student outcomes?
Learn more about our school licenses here.
Find the Ph of a Solution of 0.013 M Hno2
Source: https://www.albert.io/blog/how-to-calculate-ph-in-chemistry/
0 Response to "Find the Ph of a Solution of 0.013 M Hno2"
Post a Comment